多元回歸分析檢視原始碼討論檢視歷史
| 多元回歸分析 |
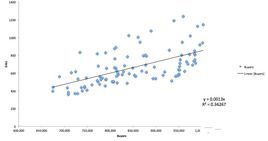 |
多元回歸分析是指分析因變量和自變量之間關係,回歸分析的基本思想是: 雖然自變量和因變量之間沒有嚴格的、確定性的函數關係,但可以設法找出最能代表它們之間關係的數學表達形式。
簡介
⑴ 確定幾個特定的變量之間是否存在相關關係,如果存在的話,找出它們之間合適的數學表達式;
⑵ 根據一個或幾個變量的值,預測或控制另一個變量的取值,並且可以知道這種預測或控制能達到什麼樣的精確度;
⑶ 進行因素分析。例如在對於共同影響一個變量的許多變量(因素)之間,找出哪些是重要因素,哪些是次要因素,這些因素之間又有什麼關係等等。
評價
摺疊回歸方程 回歸分析有很廣泛的應用,例如實驗數據的一般處理,經驗公式的求得,因素分析,產品質量的控制,氣象及地震預報,自動控制中數學模型的制定等等。
多元回歸分析是研究多個變量之間關係的回歸分析方法,按因變量和自變量的數量對應關係可劃分為一個因變量對多個自變量的回歸分析(簡稱為"一對多"回歸分析)及多個因變量對多個自變量的回歸分析(簡稱為"多對多"回歸分析),按回歸模型類型可劃分為線性回歸分析和非線性回歸分析。
本"多元回歸分析原理"是針對均勻設計3.00軟件的使用而編制的,它不是多元回歸分析的全面內容,欲了解多元回歸分析的其他內容請參閱回歸分析方面的書籍。
回歸分析
重難點:了解聚類分析的基本思想、方法及其簡單應用;了解回歸的基本思想、方法及其簡單應用.
考綱要求:①了解聚類分析的基本思想、方法及其簡單應用.
②了解回歸的基本思想、方法及其簡單應用.。[1]