強質數檢視原始碼討論檢視歷史
 |
在數學中, 強素數是指具有某些特性的素數[1] 。強素數的定義在密碼學和數論中是不同的(但有一定的關聯)。
數論上的定義
在數論中,如果一個素數<math>p</math>比它相鄰的兩個素數的平均數要大,則我們稱<math>p</math>為強素數。 換句話說,一個強素數是這樣的素數:和它前面的相鄰素數比較,它總是更靠近在它後面的下一個素數。 或者用代數的語言來說,對於素數p_n(n是它在所有素數的有序集合中的索引),則p_n為強素數當且僅當p_n > p_{n - 1} + p_{n + 1} \over 2。 下面列出最小的幾個強素數:
11, 17, 29, 37, 41, 59, 67, 71, 79, 97, 101, 107, 127, 137, 149, 163, 179, 191, 197, 223, 227, 239, 251, 269, 277, 281, 307, 311, 331, 347, 367, 379, 397, 419, 431, 439, 457, 461, 479, 487, 499 *id=A051634
例如,17是第7個素數。而第6個和第8個素數分別是13和19,加起來是32,平均值是16,小於17。所以17是一個強素數。
在一對孿生素數(p, p+2>)里,當p>5時,p總是強素數。這是因為p-2必能被3整除,所以不可能是素數。
有些素數既符合密碼學的強素數定義也符合數論上的強素數定義。比方說, 439351292910452432574786963588089477522344331 就是一個數論意義上的強素數,因為與它相鄰的兩的素數的平均數比它小62。如果沒有電腦的話,這個數也可以是一個密碼學意義上的強素數。這是因為 439351292910452432574786963588089477522344330 有一個大質因數 1747822896920092227343 (而這個質因數減去1後又有一個大質因數 1683837087591611009 ),而 439351292910452432574786963588089477522344332 也有一個大質因數 864608136454559457049 (而它減去1後也有大質因數 105646155480762397 )。 就算是用比較先進的算法,用紙和筆也很難分解這樣大的數。但對於現代的計算機代數系統來說,分解這樣的數是很容易的事。所以真正的密碼學意義上的強素數比前例中的這些數還要大很多。
強素數在密碼學上的應用
基於整數分解的密碼系統
有人建議在RSA密碼系統的鑰匙生成算法中,模數<math>n</math>應該是兩個強素數之積。這樣,如果用Pollard的p-1質因數分解算法來分解<math>n = pq</math>就會變得不可行。由於這個原因,ANSI X.31標準要求,在為基於RSA的數字簽名算法生成鑰匙的時候,必須用強素數。但是,強素數並不能保證n在用其它更新的算法來分解時也一樣難以分解。例如Lenstra的橢圓分解法|Lenstra elliptic curve factorization和普通數域篩選法。考慮到為了生成強素數需要用去更多的時間,RSA Security目前並不建議在鑰匙生成算法中使用強素數。Rivest和Silverman == 密碼學中的定義 ==
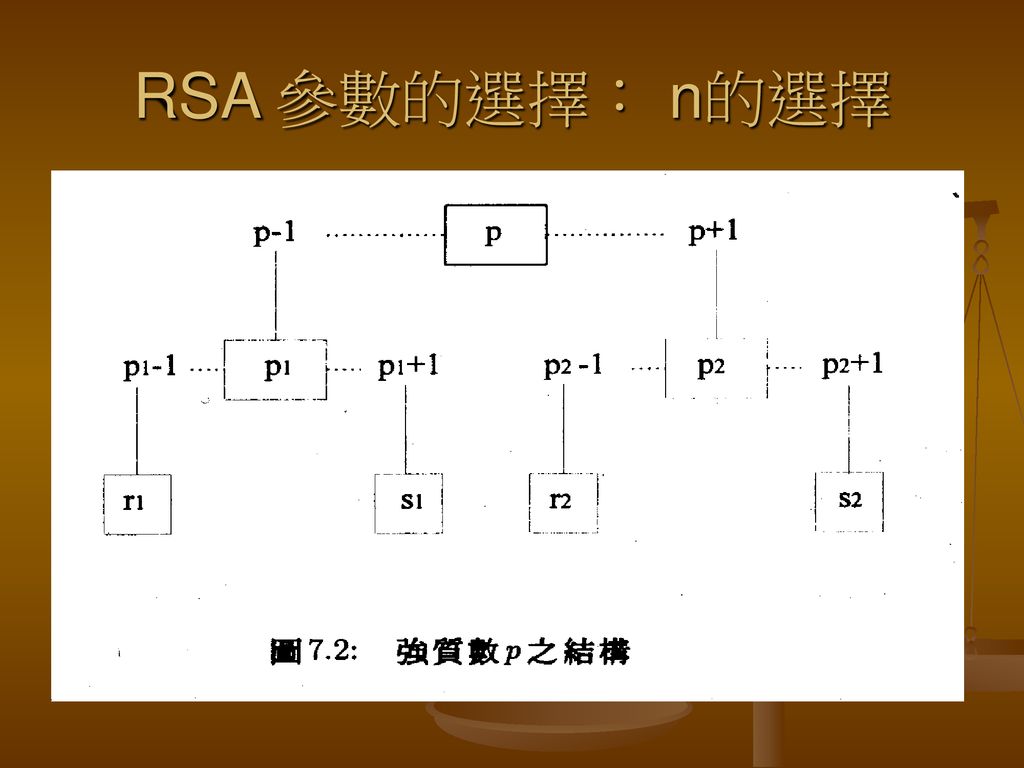
在密碼學中,一個素數<math>p</math>在滿足下列條件時被稱為強素數:
- p 必須是很大的數。
- p-1 有很大的質因數。也就是說,對於某個整數a_1以及大素數q_1,我們有p = a_1 q_1 + 1。
- q_1-1 有很大的質因數。也就是說,對於某個整數a_2以及大素數q_2,我們有q_1 = a_2 q_2 + 1。
- p+1 有很大的質因數。也就是說,對於某個整數a_3以及大素數q_3,我們有p = a_3 q_3 - 1。
有時,當一個素數隻滿足上面一部分條件的時候,我們也稱它是強素數。而有的時候,我們則要求加入更多的條件。例如,我們可以要求a_1 = 2,或者a_2 = 2。從這個角度上來說,很大的安全素數可以看作是強素數的一種。也給出了類似但更細緻的論述。
基於離散對數的密碼系統
1978年由 Stephen Pohlig 和 Martin Hellman 證明,如果 p-1 的所有質因數都小於 <math>log^c p</math>,那麼解決模數為<math>p</math>的 離散對數 問題就屬於 P問題。所以,對於基於離散對數的密碼系統,比如數字簽名算法(即DSA),我們就要求 p-1 至少要有一個大質因數。
其它
要注意的是,判斷一個偽素數是否是強偽素數時,我們看的是它除以某個基數的冪之後的餘數,而不是看它和相鄰的偽素數的平均數那個較大。
在數論中,如果一個素數剛好等於其相鄰素數的平均數,那麼我們把這個素數叫做平衡質數。如果它比平均數小,則叫做弱素數。