非線性回歸檢視原始碼討論檢視歷史
| 非線性回歸 |
 |
非線性回歸是回歸函數關於未知回歸係數具有非線性結構的回歸。常用的處理方法有回歸函數的線性迭代法、分段回歸法、迭代最小二乘法等。非線性回歸分析的主要內容與線性回歸分析相似。
簡介
所謂回歸分析法,是在掌握大量觀察數據的基礎上,利用數理統計方法建立因變量與自變量之間的回歸關係函數表達式(稱回歸方程式)。回歸分析中,當研究的因果關係只涉及因變量和一個自變量時,叫做一元回歸分析;當研究的因果關係涉及因變量和兩個或兩個以上自變量時,叫做多元回歸分析。此外,回歸分析中,又依據描述自變量與因變量之間因果關係的函數表達式是線性的還是非線性的,分為線性回歸分析和非線性回歸分析。通常線性回歸分析法是最基本的分析方法,遇到非線性回歸問題可以藉助數學手段化為線性回歸問題處理。
評價
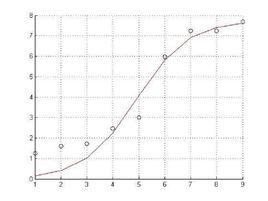
例1:1790-1960某國人口變化數據:注意:即便線性方程對對觀測數據擬合相當好,但有關誤差項的獨立性和方差假設有可能被破壞。原因是時間序列的數據誤差項往往不獨立,誤差項大小有可能根據數據總體的大小而變化,意思就是,即便適合這個樣本的觀測量的方程,但是,不適合總體。根據經驗,人口增長模型不能被轉化為線性模型,所以,可以利用曲線回歸或者非線性回歸。進一步比較究竟是曲線回歸好還是非線性回歸好,需要建立新的殘差變量,這一步並不難,就是在spss中,相應分析的保存子對話框中建立新的對應模型的變量。其實,有一個萬能公式:spss中,所有的「保存」對話框的功能都是,在二維表窗口也就是spss的盛放數據窗口中建立新變量,這個新變量有默認名,是相應分析的重要結果。保存新變量以後,需要根據殘差的序列圖進行判斷:最平穩的就是最合適的。 例2:血中藥物濃度和時間曲線呈非線性關係。 這個是根據專業背景知識而判斷。藥物不可能馬上見效,也許在血液中逐步或者突然見效。 例3:身高和體重,在青少年中,是呈直線關係,因為,青少年在不斷成長,但是,對於整個人的生命周期,確是曲線關係 因為,成年人的身高一般是確定的。 像這樣的例子根本用直線回歸擬合不了,也稱為非本質線性模型。對於這種實際情況,可以使用非線性回歸的分段模型。最終目的是使殘差平方和最小。也就是在圖形中跟大多數散點接近。[1]