干涉 (物理學)

楊氏雙縫干涉 圖片來自slidesplayer

干涉（interference）在物理學中，指的是兩列或兩列以上的波在空間中重疊時發生疊加，從而形成新波形的現象。

例如採用分束器將一束單色光束分成兩束後，再讓它們在空間中的某個區域內重疊，將會發現在重疊區域內的光強並不是均勻分布的：其明暗程度隨其在空間中位置的不同而變化，最亮的地方超過了原先兩束光的光強之和，而最暗的地方光強有可能為零，這種光強的重新分布被稱作「干涉條紋」。在歷史上，干涉現象及其相關實驗是證明光的波動性的重要依據，但光的這種干涉性質直到十九世紀初才逐漸被人們發現，主要原因是相干光源的不易獲得。

為了獲得可以觀測到可見光干涉的相干光源，人們發明製造了各種產生相干光的光學器件以及干涉儀，這些干涉儀在當時都具有非常高的測量精度：阿爾伯特·邁克耳孫就藉助邁克耳孫干涉儀完成了著名的邁克耳孫－莫雷實驗，得到了以太風觀測的零結果。邁克耳孫也利用此干涉儀測得標準米尺|International prototype metre的精確長度，並因此獲得了1907年的諾貝爾物理學獎。而在二十世紀六十年代之後，激光這一高強度相干光源的發明使光學干涉測量技術得到了前所未有的廣泛應用，在各種精密測量中都能見到激光干涉儀的身影。現在人們知道，兩束電磁波的干涉是彼此振動的電場強度矢量疊加的結果，而由於光的波粒二象性，光的干涉也是光子自身的幾率幅疊加的結果。

目錄

干涉的條件

兩列波在同一介質中傳播發生重疊時，重疊範圍內介質的質點 同時受到兩個波的作用。若波的振幅不大，此時重疊範圍內介質質點的振動位移等於各別波動所造成位移的矢量和，這稱為波的疊加原理。若兩波的波峰（或波谷）同時抵達同一地點，稱兩波在該點同相，干涉波會產生最大的振幅，稱為相長干涉（建設性干涉）；若兩波之一的波峰與另一波的波谷同時抵達同一地點，稱兩波在該點反相，干涉波會產生最小的振幅，稱為相消干涉（摧毀性干涉）。

理論上，兩列無限長的單色波的疊加總是能產生干涉，但實際物理模型中產生的波列不可能是無限長的，並從波產生的微觀機理來看，波的振幅和相位都存在有隨機漲落，從而現實中不存在嚴格意義的單色波。例如太陽所發出的光波出自於光球層的電子與氫原子的相互作用，每一次作用的時間都在10^-9秒的數量級，則對於兩次發生時間間隔較遠所產生的波列而言，它們無法彼此發生干涉。基於這個原因，可以認為太陽是由很多互不相干的點光源組成的擴展光源。從而，太陽光具有非常寬的頻域，其振幅和相位都存在着快速的隨機漲落，通常的物理儀器無法跟蹤探測到變化如此之快的漲落，因此無法通過太陽光觀測到光波的干涉。類似地，對於來自不同光源的兩列光波，如果這兩列波的振幅和相位漲落都是彼此不相關的，稱這兩列波不具有相干性。相反，如果兩列光波來自同一點光源，則這兩列波的漲落一般是彼此相關的，此時這兩列波是完全相干的。

如要從單一的不相干波源產生相干的兩列波，可以採用兩種不同的方法：一種稱為波前分割法，即對於幾何尺寸足夠小的波源，讓它產生的波列通過並排放置的狹縫，根據惠更斯－菲涅耳原理，這些在波前上產生的子波是彼此相干的；另一種成為波幅分割法，用半透射、半反射的半鍍銀鏡，可以將光波一分為二，製造出透射波與反射波。如此產生的反射波和透射波來自於同一波源，並具有很高的相干性，這種方法對於擴展波源同樣適用。

楊氏雙縫

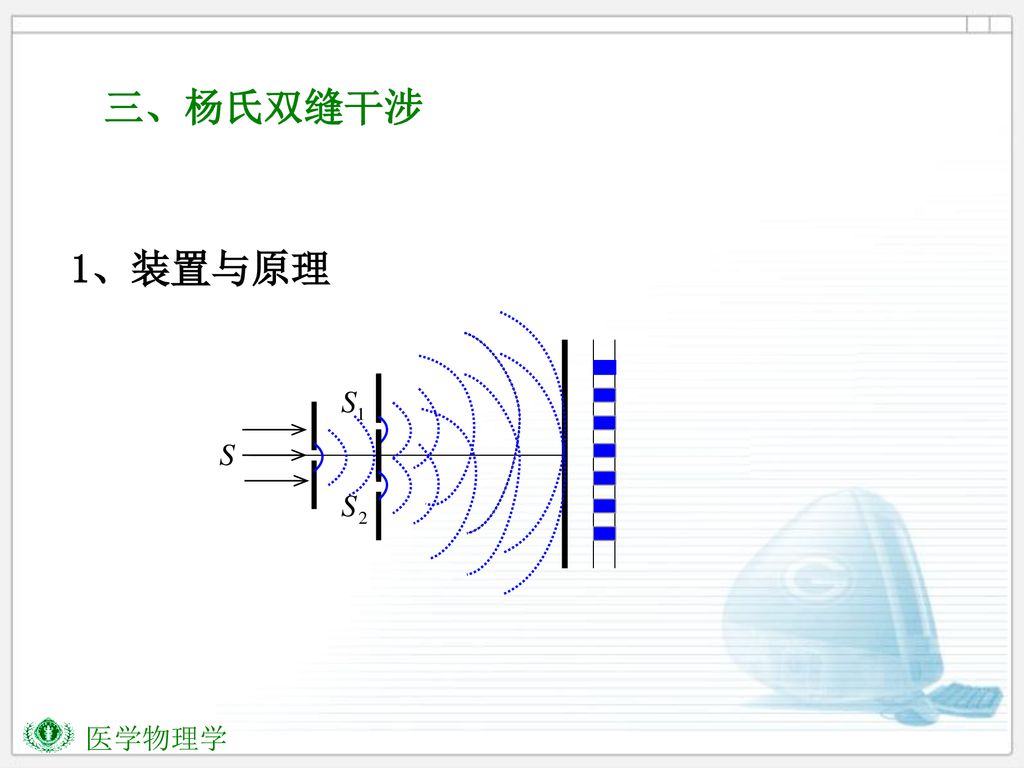
英國物理學者托馬斯·楊於1801年做實驗演示光的干涉演示，稱為楊氏雙縫實驗。這實驗對於光波動說給出有力支持，由於實驗觀測到的干涉條紋是艾薩克·牛頓所代表的光微粒說無法解釋的現象，雙縫實驗使大多數的物理學家從此逐漸接受了光波動說。楊氏雙縫的實驗設置如右圖所示，從一個點光源出射的單色波傳播到一面有兩條狹縫的擋板，兩條狹縫到點光源的距離相等，並且兩條狹縫間的距離很小。由於點光源到這兩條狹縫的距離相等，這兩條狹縫就成為了同相位的次級單色點光源，從它們出射的相干光發生干涉，因此可以在遠距離的屏上得到干涉條紋。

如果兩條狹縫之間的距離為a，狹縫到觀察屏的垂直距離為d，則根據幾何關係，在觀察屏上以對稱中心點為原點，坐標為(x, y),處兩束相干光的光程分別為

L_1 = \sqrt{d^2 + y^2 + (x - \frac{a}{2})^2}\,

L_2 = \sqrt{d^2 + y^2 + (x + \frac{a}{2})^2}\,

當狹縫到觀察屏的垂直距離d,遠大於x,時，這兩條光路長度的差值可以近似在圖上表示為：從狹縫1向光程2作垂線所構成的直角三角形中，角\alpha^{\prime}\,所對的直角邊\Delta s\。而根據幾何近似，這段差值為

Delta s = a \sin \alpha^{\prime} \approx a \frac{x}{d}\,

如果實驗在真空或空氣中進行，則認為介質折射率等於1，從而有光程差Delta L = \Delta s = a \frac{x}{d}\,相位差delta = \frac{2\pi}{\lambda}\frac{ax}{d}\。

根據前文結論，當相位差delta\,等於2m\pi, \quad |m| = 0, 1, 2,...\,時光強有極大值，從而當x = \frac{md\lambda}{a}, \quad |m| = 0, 1, 2,...\,時有極大值；當相位差\delta\,等於2m\pi, \quad |m| = \frac{1}{2}, \frac{3}{2}, \frac{5}{2},...\,時光強有極小值，從而當x = \frac{md\lambda}{a}, \quad |m| = \frac{1}{2}, \frac{3}{2}, \frac{5}{2},時有極小值。從而楊氏雙縫干涉會形成等間距的明暗交替條紋，間隔為frac{d\lambda}{a}\。

若在雙縫干涉中增加狹縫在兩條狹縫連線上的線寬，以至於狹縫無法看作是一個點光源，此時形成的擴展光源可以看作是多個連續分布的點光源的集合。這些點光源由於彼此位置不同，在屏上同一點將導致不同的相位差，將有可能導致各個點光源干涉的極大值和極小值點重合，這就導致了條紋可見度的下降。

菲涅耳雙面鏡

菲涅耳雙面鏡（Fresnel double mirror）是一種可以直接產生兩個相干光源的儀器。菲涅耳雙面鏡是兩個長度相同的平面鏡M1、M2的組合，兩個平面鏡的擺放相對位置成一個很小的傾角α。當光波從點光源S的位置入射到兩個鏡面發生各自的反射後，分別形成了兩個虛像S1和S2。由於它們是同一光源的虛像，因此是相干光源，左圖中藍色陰影的部分即為兩束光的干涉區域。

從圖中可見菲涅耳雙面鏡干涉的幾何關係與楊氏雙縫相同，因此只要求得兩個虛像間的距離d就可以推知干涉條紋的位置。如果設光源S到兩個平面鏡交點A的距離為b，根據鏡面對稱可知兩個相干光源到鏡面交點的距離也等於b，即S_1A = S_2A = SA = b，

而虛光路S₁A、S₂A和平分線（圖中水平的點劃線）的夾角都等於平面鏡傾角α，從而有d = 2b\sin \alpha\。

這個距離等效於楊氏雙縫中兩條狹縫的間距，代入上文中公式即可得到干涉條紋的位置。光波入射到兩個鏡面時各自都會發生\pi\,的反射相變，從而不會影響兩者最終的相位差，因此菲涅耳雙面鏡干涉條紋的形狀與楊氏雙縫完全相同，都是等間距的明暗相間條紋，中間為零級亮紋。