平移
| 平移 |
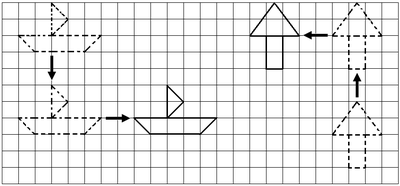 |
平移 是指在平面內,將一個圖形上的所有點都按照某個直線方向做相同距離的移動,這樣的圖形運動叫做圖形的平移運動,簡稱平移。平移不改變圖形的形狀和大小。圖形經過平移,對應線段相等,對應角相等,對應點所連的線段相等。 它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若是一個已知的向量,是空間中一點,平移。
基本信息
中文名稱 平移 [1]
外文名稱 translation
領域 幾何數學
定義
將所有點平移兩次,結果可用一次平移表示,即,因此所有平移的集是一個群,稱為平移群。這個群和空間同構,又是歐幾里德群的正規子群。
在仿射幾何,平移是將物件的每點向同一方向移動相同距離。
它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若是一個已知的向量,是空間中一點,平移。
將同一點平移兩次,結果可用一次平移表示,即,因此所有平移的集是一個群,稱為平移群。這個群和空間同構,又是歐幾里德群的正規子群。
T對E的商群與正交群同構……
基本性質
經過平移,對應線段平行(或共線)且相等,對應角相等,對應點所連接的線段平行(共線)且相等;
平移變換不改變圖形的形狀、大小和方向(平移前後的兩個圖形是全等形)。
(1)圖形平移前後的形狀和大小沒有變化,只是位置發生變化。
(2)圖形平移後,對應點連成的線段平行(或在同一直線上)且相等。
(3)多次連續平移相當於一次平移。
(4)偶數次對稱後的圖形等於平移後的圖形。
(5)平移是由方向和距離決定的。
(6)經過平移,對應線段平行(或共線)且相等,對應角相等,對應點所連接的線段平行(或共線)且相等。
這種將圖形上的所有點都按照某個方向作相同距離的位置移動,叫做圖形的平移運動,簡稱為平移
平移的條件:確定一個平移運動的條件是平移的方向和距離。
平移
是指在平面內,將一個圖形上的所有點都按照某個方向作相同距離的移動,這樣的圖形運動叫做圖 形的平移運動,簡稱平移。平移不改變物體的形狀和大小。平移可以不是水平的。也就是把一個圖形沿着某個方向移動一定的距離,這種移動叫做平移變換,簡稱平移.。
三個要點
1 原來的圖形的形狀和大小和平移後的圖形是全等的。
2 平移的方向。(東南西北,上下左右,東偏南n度,東偏北n度,西偏南n度,西偏北n度)
3 平移的距離。(長度,如7厘米,8毫米等)
平移作用
1.通過簡單的平移可以構造精美的圖形。也就是花邊,通常用於裝飾,過程就是複製-平移-粘貼。
2.平移常與平行線有關,平移可以將一個角,一條線段,一個圖形平移到另一個位置,是分散的條件集中到一個圖形上,使問題得到解決。
總體歸納
1 把一個圖形整體沿某一直線方向移動,會得到一個新的圖形,新圖形與原圖形的形狀和大小完全相同。
2 新圖形中的每一點,都是由原圖形中的某一點移動後得到的,這兩個點是對應點。連接各組對應點的線。 段。 平行且相等(或在同一直線上)。
參考來源