數制

來自 搜狐網 的圖片

數制是中國的一個科技名詞。

語言一發即逝，不留痕跡。當人類意識到需要把說出的話記下來時，就發明了文字。在世界範圍內，曾經獨立形成的古老文字除我們的漢字外，還有埃及的聖書字、兩河流域的楔形文字、古印度的印章文字以及中美洲的瑪雅文。後來，這些古老文字的命運各不相同，或因某種歷史原因而消亡，如瑪雅文；或因文字的根本變革而遭廢棄，如楔形文、聖書字，只漢字沿用至今，而且古今傳承的脈絡清晰可見，成了中華民族文化的良好載體。

目錄

名詞解釋

數制也稱為「計數制」，是用一組固定的符號和統一的規則來表示數值的方法。任何一個數制都包含兩個基本要素：基數和位權。

「量」才是本質，數只是「量」在某個特定的符號系統中指稱，一個量可以在許多種符號系統中表示出來，符號只是指稱。 （就像人才是本質，名字只是在不同的場景下的指稱，可能同學喜歡叫你小名，老師卻喜歡叫你大名，不管大名還是小名都指的是你）

不同的數制間可以進行進制轉換。

數碼

數制中表示基本數值大小的不同數字符號。例如，十進制有10個數碼：0、1、2、3、4、5、6、7、8、9。

基數

數制所使用數碼的個數。例如，二進制的基數為2；十進制的基數為10。

位權

數制中某一位上的1所表示數值的大小（所處位置的價值）。例如，十進制的123，1的位權是100，2的位權是10，3的位權是1。二進制中的 1011 (一般從左向右開始)，第一個1的位權是8，0的位權是4，第二個1的位權是2，第三個1的位權是1

計數

計數的規則。在人們使用最多的進位計數制中，表示數的符號在不同的位置上時所代表的數的值是不同的。

十進制

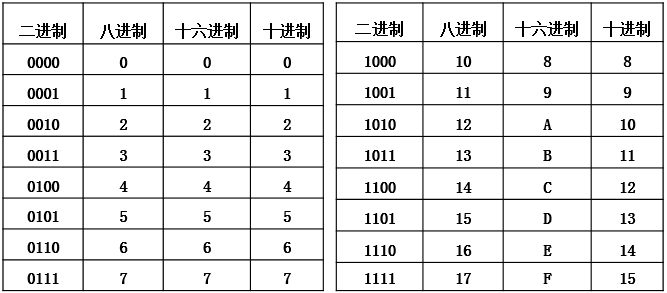
人們在日常生活中最熟悉的進位計數制。在十進制中，數用0，1，2，3，4，5，6，7，8，9這十個符號來描述。計數規則是逢十進一。

二進制

在計算機系統中採用的進位計數制。在二進制中，數用0和1兩個符號來描述。計數規則是逢二進一，借一當二。

十六進制

人們在計算機指令代碼和數據的書寫中經常使用的數制。在十六進制中，數用0，1，…，9和A,B,…，F（或a，b，…，f）16個符號來描述。計數規則是逢十六進一。