豪斯多夫空間
| 豪斯多夫空間 |
 |
豪斯多夫空間,在拓撲學和相關的數學分支中,豪斯多夫空間、分離空間或T2 空間是其中的點都"由鄰域分離"的拓撲空間。在眾多可施加在拓撲空間上的分離公理中,"豪斯多夫條件"是最常使用和討論的。它蘊涵了序列、網和濾子的極限的唯一性。豪斯多夫得名於拓撲學的創立者之一費利克斯·豪斯多夫。豪斯多夫最初的拓撲空間定義把豪斯多夫條件包括為公理。
目錄
簡介
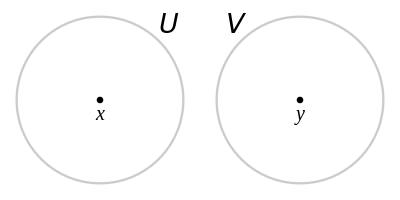
假設 X 是拓撲空間。設 x 和 y 是 X 中的點。如果存在 x 的鄰域 U 和 y 的鄰域 V 使得 U 和 V 是不相交的 (U ∩ V = ∅),我們稱 x 和 y 可以"由鄰域分離"。X 是豪斯多夫空間如果任何兩個X 的不同的點可以由鄰域分離。這是豪斯多夫空間也叫做 T2 空間和分離空間的原因。
X 是預正則空間,如果任何兩個拓撲可區分的點可以由鄰域分離。預正則空間也叫做 R1 空間。
在這些條件之間的聯繫如下。拓撲空間是豪斯多夫空間,當且僅當它是預正則空間和柯爾莫果洛夫空間的二者(就是說獨特的點是拓撲可區分的)。拓撲空間是預正則空間,當且僅當它的柯爾莫果洛夫商空間是豪斯多夫空間。
評價
豪斯多夫空間的子空間和乘積是豪斯多夫空間,[1] 但是豪斯多夫空間的商空間不必須是豪斯多夫空間。事實上,所有拓撲空間都可以實現為某個豪斯多夫空間的商。
豪斯多夫空間是 T1 空間,這意味着所有單元素集合是閉集。類似的,預正則空間是 R0 空間。
豪斯多夫空間另一個美好的性質是緊緻集合總是閉集。[2]這對於非豪斯多夫空間就可能失效(例如有其失效的 T1 空間的例子)。
豪斯多夫空間的定義聲稱點可以由鄰域分離。它蘊涵了表象上更強的東西: 在豪斯多夫空間中所有成對的不相交的緊緻集合都可以由鄰域分離。[3] 這是緊緻集合經常表現得如同點的一般規則的一個例子。
緊緻性條件與預正則一起經常蘊涵了更強的分離公理。例如,任何局部緊緻預正則空間都是完全正則空間。緊緻預正則空間是正規空間,意味着它們滿足Urysohn引理和Tietze擴張定理,並且有服從局部有限開覆蓋的單位劃分。這些陳述的豪斯多夫版本是: 所有局部緊緻豪斯多夫空間是吉洪諾夫空間,而所有緊緻豪斯多夫空間是正規豪斯多夫空間。
下列結果是關於來或到豪斯多夫空間的映射(連續函數和其他)的技術上的性質。
設 f : X → Y 是連續函數並假定 Y 是豪斯多夫空間。則 f 的圖象 是 X × Y 的閉子集。
設 f : X → Y 是函數並設 是作為 X × X 的子空間的它的核。
如果 f 是連續函數並且 Y 是豪斯多夫空間則 ker(f) 閉集。
如果 f 是開滿射而 ker(f) 是閉集則 Y 豪斯多夫空間。
如果 f 是連續開滿射(就是開商映射),則 Y 是豪斯多夫空間,當且僅當 ker(f) 是閉集。
如果 f,g : X → Y 是連續映射而 Y 豪斯多夫空間,則均衡子 在 X 是是閉集。可得出如果 Y 是豪斯多夫空間而 f 和 g 一致於 X 的稠密子集,則 f = g。換句話說,到豪斯多夫空間的連續函數確定自它們在稠密子集上的值。
設 f : X → Y 是閉滿射使得 f−1(y) 對於所有 y ∈ Y 是緊緻的。則如果 X 是豪斯多夫空間則 Y 也是。
設 f : X → Y 是商映射帶有 X 是緊緻豪斯多夫空間。則下列是等價的
Y 是豪斯多夫空間
f 是閉映射
ker(f) 是閉集[1]