採樣控制理論
| 採樣控制理論 |
 |
採樣控制理論,經典控制理論中研究採樣控制系統的組成原理、基本特性和分析設計方法的一個分支。採樣控制系統不同於連續控制系統,它的特點是系統中一處或幾處的信號具有脈衝序列或數字序列的形式。應用採樣控制,有利於提高系統的控制精度和抗干擾能力,也有利於提高控制器的利用率和通用性。
目錄
簡介
經典控制理論中研究採樣控制系統的組成原理、基本特性和分析設計方法的一個分支。採樣控制系統不同於連續控制系統,它的特點是系統中一處或幾處的信號具有脈衝序列或數字序列的形式。應用採樣控制,有利於提高系統的控制精度和抗干擾能力,也有利於提高控制器的利用率和通用性。隨着微型計算機的普及,採樣控制更顯示出其優越性。在採樣控制理論中主要採用頻率域方法,它以Z變換為數學基礎,又稱Z變換法。通過引入Z變換,在連續控制系統研究中所採用的許多基本概念(如傳遞函數、頻率響應等)和分析設計法(如穩定性和過渡過程的分析方法、控制系統校正方法等),都可經過適當的修正而推廣應用於採樣控制系統。在現代控制理論中,與採樣控制系統屬於同一範疇的離散系統的分析主要採用時間域方法,它是建立在狀態空間描述的基礎上的,又稱狀態空間法。
評價
採樣控制系統按組成原理分為一般採樣控制系統和數字控制系統。
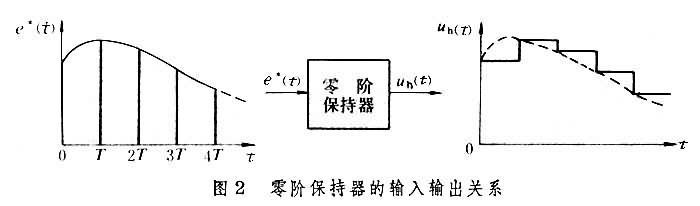
一般採樣控制系統這種系統的典型的組成方式如圖1,圖中量測元件的作用是把受控對象的輸出變量變換為適當的物理量以實現反饋,校正裝置的作用是使控制系統獲得滿意的性能。與一般連續型反饋控制系統不同的是,它包含信號採樣和復原的裝置。實現採樣的裝置稱為採樣器,通常接於誤差信號e(t)的作用點。採樣器有多種採樣形式,最常見的是採樣周期為常數的等速採樣。當系統中包含有幾個採樣器時,它們的採樣周期必須相等,相位必須同步。一切具有開關功能的裝置,如機械開關、數字電路、掃描裝置等都可用來作為採樣器。連續信號e(t)通過採樣器時, 隨着採樣開關的重複閉合和斷開, 變換為一個周期脈衝序列e(t)。e(t)的值在採樣開關閉合瞬間等於e(t),而在開關斷開時等於零。由於受控對象常常是一個具有連續特性的系統,為了使脈衝序列e(t)中的高頻分量不致對它構成干擾和引起機械部件的損壞,e(t)在作用於連續部件之前需要通過具有濾波功能的裝置,復原為連續信號。這類復原裝置稱為保持器。最簡單的保持器是一個低通濾波器,能將脈衝序列轉換成在兩個相鄰採樣瞬時之間保持常值的一個階梯信號(圖2),通常稱為零階保持器。它的傳遞函數為,其中T 為脈衝序列的周期。
數字控制系統數字控制系統是採樣控制系統中一種重要的類型。數字控制系統(圖3)除了包含信號的採樣和復原外,還包含信號量化和復原的過程。把信號幅值變換為數字計算機可接受的數碼,稱為量化。相應的部件稱為模數變換器,簡稱A/D。使數碼恢復為信號幅值的裝置則稱為數模變換器,簡稱D/A。通常,數模變換器同時也具備保持器的功能。對信號進行量化的結果使得有可能採用數字計算機作校正裝置,通過編制相應的程序,以實現按控制規律所要求的信號校正。數字校正裝置在通用性和精確性方面具有明顯的優越性。
採樣過程的數字處理為簡化問題處理,在採樣控制理論中,把連續信號e(t)經過採樣器得到的周期性脈衝序列e(t)理想化為一個數字函數序列,它的表達式為
式中T 為採樣周期,e(kT)是連續信號e(t)在採樣瞬時kT(k=0,1,2,...)的值,符號Σ表示所列變量的求和,δ(t-kT)稱為作用於kT時刻的單位脈衝函數,它的定義是:
為了使採樣信號能恢復到原連續信號,採樣周期T的值不能任意選取,必須符合香農定理所給出的條件,即要求不等式成立,其中ω1是原連續信號的幅頻譜的上限頻率,它的含義是信號的傅里葉變換後振盪分量中不包含頻率大於ω1 的諧波分量。
採樣系統的基本特性在採樣控制理論中,系統的分析和設計都是建立在脈衝傳遞函數的基礎上的。脈衝傳遞函數表徵採樣系統的輸出輸入關係,這個關係用系統輸出採樣信號的Z變換與輸入採樣信號的Z變換之比來表示。
採樣系統的穩定性如果已知採樣系統的脈衝傳遞函數G(z)=N(z)/D(z)。那麼系統穩定的充分必要條件是特徵方程D(z)=0的根均位於z 複數平面上圍繞原點的半徑為1的單位圓內。常用的判斷採樣系統穩定性的方法有代數穩定判據、奈奎斯特穩定判據和根軌跡法。
①代數穩定判據利用雙線性變換
,可把z複數平面上單位圓內部映射到r複數平面上除虛軸以外的左半平面內。因此D(z)=0的根均位於z平面的單位圓內等價於
的根均位於r平面的左半平面內。通過對D(r)=0運用代數穩定判據,可判斷採樣系統的穩定性。
②奈奎斯特穩定判據對反饋中不包含環節的採樣控制系統,用
表示斷開反饋(見反饋控制系統)時的開環脈衝傳遞函數。DO(z)=0為系統的開環特徵方程。當複數變量z由z平面的(1,j0)點出發沿單位圓逆時針方向變化時,在G0(z)複數平面上作出相應的G0(z)的軌線。那麼,當 G0(z)軌線沿逆時針方向包圍(-1,j0)點的次數恰好等於D0(z)=0在單位圓內的根的個數時,採樣控制系統是穩定的。這是連續控制系統的奈奎斯特穩定判據的推廣。
③根軌跡法把連續控制系統的根軌跡的作圖步驟(見根軌跡法)運用於採樣系統的開環脈衝傳遞函數G0(z),可分析採樣反饋系統的特徵方程根的分布,從而可用來判斷系統的穩定性。
採樣系統的瞬態響應採樣系統的瞬態響應是指典型輸入作用下系統輸出的響應。用R(z)表示輸入作用r(t)的Z變換,G(z)表示系統的脈衝傳遞函數,則輸出響應c(t)的Z變換C(z)=G(z)R(z)。通過對C(z)求Z變換的反變換即可定出c(t)。通常分析結果只能反映瞬態響應在採樣時刻kT(k=0,1,2,...)上的函數值。
採樣控制系統的校正校正是通過引入某種裝置使控制系統具有所期望的性能指標的方法。常用的校正裝置類型有模擬校正裝置和數字校正裝置。在一般採樣控制系統中採用模擬校正裝置,它們常是電阻和電容組成的一個網絡。在數字控制系統中採用數字校正裝置,它用數字處理或數字計算的方式實現對信號的校正,常可通過編制相應的算法程序由數字計算機來完成。數字控制器的優點,是能以很高的精度來實現所要求的複雜運算,而且只需要通過改變程序就可產生不同的控制校正作用。相應的連續控制系統校正裝置的設計方法(見控制系統校正方法),在經過適當的修正後,可用於設計採樣控制系統的校正裝置。[1]