一階電路檢視原始碼討論檢視歷史
| 一階電路 |
 |
在一個電路簡化後(如電阻的串並聯,電容的串並聯,電感的串並聯化為一個元件),只含有一個電容或電感元件(電阻無所謂)的電路叫一階電路。主要是因為這樣的電路的Laplace等效方程中是一個一階的方程。
基本內容
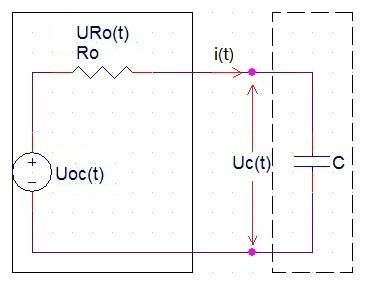
1.任意激勵下一階電路的通解一階電路,a.b之間為電容或電感元件,激勵Q(t)為任意時間函數,求一階電路全響應一階電路的微分方程和初始條件為:
df(t)dt+p(t)f(t)=?(t)
(1) f(0+)=u0其中p(t)=1τ,
用「常數變易法」求解。
令f(t)=u(t)e-∫p(t)dt,代入方程得
u(t)=∫(t)e∫p(t)dtdt+c1f(t)=c1e-∫p(t)dt+e-∫p(t)dt
∫(t)e∫p(t)dtdt=fh(t)+fp(t)
(2)常數由初始條件決定.其中fh(t)、fp(t)分別為暫態分量和穩態分量。
2.三要素公式通用形式用p(t)=1τ和初始條件f(0+)代入(2)式有c1=f(0+)-fp(0+)f(t)=fp(t)+[f(0+)-fp(0+)]e-1
上式中每一項都有確定的數學意義和物理意義.fp(t)=e-1τ∫(t)e1τdt在數學上表示方程的特解,即t~∞時的f(t),所以,在物理上fp(t)表示一個物理量的穩態。(隨t作穩定變化)。
fh(t)=c1e-1τ在數學上表示對應齊次方程的通解,是一個隨時間作指數衰減的量,當時t~∞,fh(t)~0,在物理上表示一個暫態,一個過渡過程。
c1=f(0+)-fp(0+),其中fp(0+)表示穩態解在t=0時的值.τ=RC(或L/R),表示f(t)衰減的快慢程度,由元件參數決定.
3.穩態解的求取方法由於穩態解是方程的特解,由上面的討論可知:
fp(t)=e-1τ∫(t)e1τdt
對任意函數可直接積分求出.其方程和初始條件為:
didt+RLi=UmLcos(ωt+φu)i(0+)=I0ip(t)=e-LtR∫UmLcos(ωt+φu)eRtLdt.
用分步積分法求得ip(t)=UmR2+ω2L2cos(ωt+φu+θ),其中θ=tg-1(ωLR)ip(0+)=UmR2+ω2L2cos(φu+θ).2)由於穩態解是電路穩定後的值,對任意函數可用電路的穩態分析法求出.
如上題,使用相量法,有:I・=U・sZ=UmR2+ω2L2∠(φu+θ),ip(t)=UmR2+ω2L2cos(ωt+φu+θ).ip(0+)=UmR2+ω2L2cos(φu+θ).3)也可用試探法(待定係數法)求出fp(t).如上題中,可以令i=Imcos(ωt+Ψ),代入方程得,Im=UmR2+ω2L2,Ψ=φu+θ,ip(t)=UmR2+ω2L2=cos(ωt+φu+[1]