流形
| 流形 |
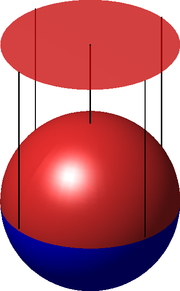 |
流形(Manifold),是局部具有歐氏空間性質的空間。而實際上歐氏空間就是流形最簡單的實例。像地球表面這樣的球面是一個稍為複雜的例子。一般的流形可以通過把許多平直的片折彎並粘連而成。
目錄
簡介
流形在數學中用於描述幾何形體,它們提供了研究可微性的最自然的舞台。物理上,經典力學的相空間和構造廣義相對論的時空模型的四維偽黎曼流形都是流形的實例。他們也用於位形空間(configurationspace)。環面(torus)就是雙擺的位形空間。
如果把幾何形體的拓撲結構看作是完全柔軟的,因為所有變形(同胚)會保持拓撲結構不變,而把解析簇看作是硬的,因為整體的結構都是固定的(譬如一個1維多項式,如果你知道(0,1)區間的取值,則整個實屬範圍的值都是固定的,局部的擾動會導致全局的變化),那麼我們可以把光滑流形看作是介於兩者之間的形體,其無窮小的結構是硬的,而整體結構是軟的。這也許是中文譯名流形的原因(整體的形態可以流動),該譯名由著名數學家和數學教育學家江澤涵引入。這樣,流形的硬度使它能夠容納微分結構,而它的軟度使得它可以作為很多需要獨立的局部擾動的數學和物理上的模型。
流形可以視為近看起來象歐氏空間或其他相對簡單的空間的物體。例如,人們曾經以為地球是平坦的,因為我們相對於地球很小,這是一個可以理解的假象。所以,一個理想的數學上的球在足夠小的區域也象一個平面,這使它成為一個流形。但是球和平面有很不相同的整體結構:如果你在球面上沿一個固定方向走,你最終回到起點,而在一個平面上,你可以一直走下去。
一個曲面是二維的。但是,流形可以有任意維度。其他的例子有,一根線的圈(一維的)以及三維空間中的所有旋轉(三維的)。旋轉所組成的空間的例子表明流形可以是一個抽象空間。流形的技術使得我們能夠獨立的考慮這些對象,從某種意義上來講,我們可以有一個不依賴於任何其他空間的球。
局部的簡單性是一個很強的要求。例如,我們不能在球上吊一個線並把這個整體叫做一個流形;包含把線粘在球上的那一點的區域都不是簡單的—既不是線也不是面—無論這個區域有多小。
我們用收集在地圖集中的平的地圖在地球上航行。類似的,我們可以用在數學圖集中的數學地圖(稱為坐標圖)來描述一個流形。通常不可能用一張圖來描述整個流形,這是因為流形和建造它的模型所用的簡單空間在全局結構上的差異。當使用多張圖來覆蓋流形的時候,我們必須注意它們重疊的區域,因為這些重疊包含了整體結構的信息。
有很多不同種類的流形。最簡單的是拓撲流形,它們局部看來像歐氏空間。其他的變種包含了它們在使用中所需要的額外的結構。例如,一個微分流形不僅支持拓撲,而且要支持微積分。黎曼流形的思想導致了廣義相對論的數學基礎,使得人們能夠用曲率來描述時空。
評價
第一個清楚地把曲線和曲面本身構想為空間的可能是高斯,他以他的theoremaegregium('高斯絕妙定理')建立了內在的微分幾何。
黎曼是第一個廣泛的展開真正需要把流形推廣到高維的工作的人。流形的名字來自黎曼原來的德語術語Mannigfaltigkeit,WilliamKingdonClifford把它翻譯為「manifoldness」(多層)。在他的格丁根就職演說中,黎曼表明一個屬性可以取的所有值組成一個Mannigfaltigkeit。他根據值的變化連續與否對stetigeMannigfaltigkeit和離散[sic]Mannigfaltigkeit(連續流形和不連續流形)作了區分。作為stetigeMannigfaltikeiten的例子,他提到了物體顏色和在空間中的位置,以及一個空間形體的可能形狀。他把一個nfachausgedehnteMannigfaltigkeit(n次擴展的或n-維流形)構造為一個連續的(n-1)fachausgedehnteMannigfaltigkeiten堆。黎曼直覺上的Mannigfaltigkeit概念發展為今天形式化的流形。黎曼流形和黎曼曲面以他的名字命名。
交換簇的概念在黎曼的時代已經被隱含的作為複流形使用。拉格朗日力學和哈密爾頓力學,從幾何方面考慮,本質上也是流形理論。
龐加萊研究了三維流形,並提出一個問題,就是現在所謂的龐加萊猜想:所有閉簡單連通的三維流形同胚於3維球嗎?這個問題已被GrigoriPerelman解決。
HermannWeyl在1912年給出了微分流形的一個內在的定義。該課題的基礎性方面在1930年代被HasslerWhitney等人運用從19世紀下半葉就開始發展的精確的直覺理清,並通過微分幾何和李群理論得到了發展。[1]