高斯过程
 |
在概率论[1] 和统计学中,高斯过程(Gaussian process)是观测值出现在一个连续域(例如时间或空间)的随机过程。在高斯过程中,连续输入空间中每个点都是与一个正态分布的随机变量相关联。此外,这些随机变量的每个有限集合都有一个多元正态分布,换句话说他们的任意有限线性组合是一个正态分布。高斯过程的分布是所有那些(无限多个)随机变量的联合分布,正因如此,它是连续域(例如时间或空间)上函数的分布。
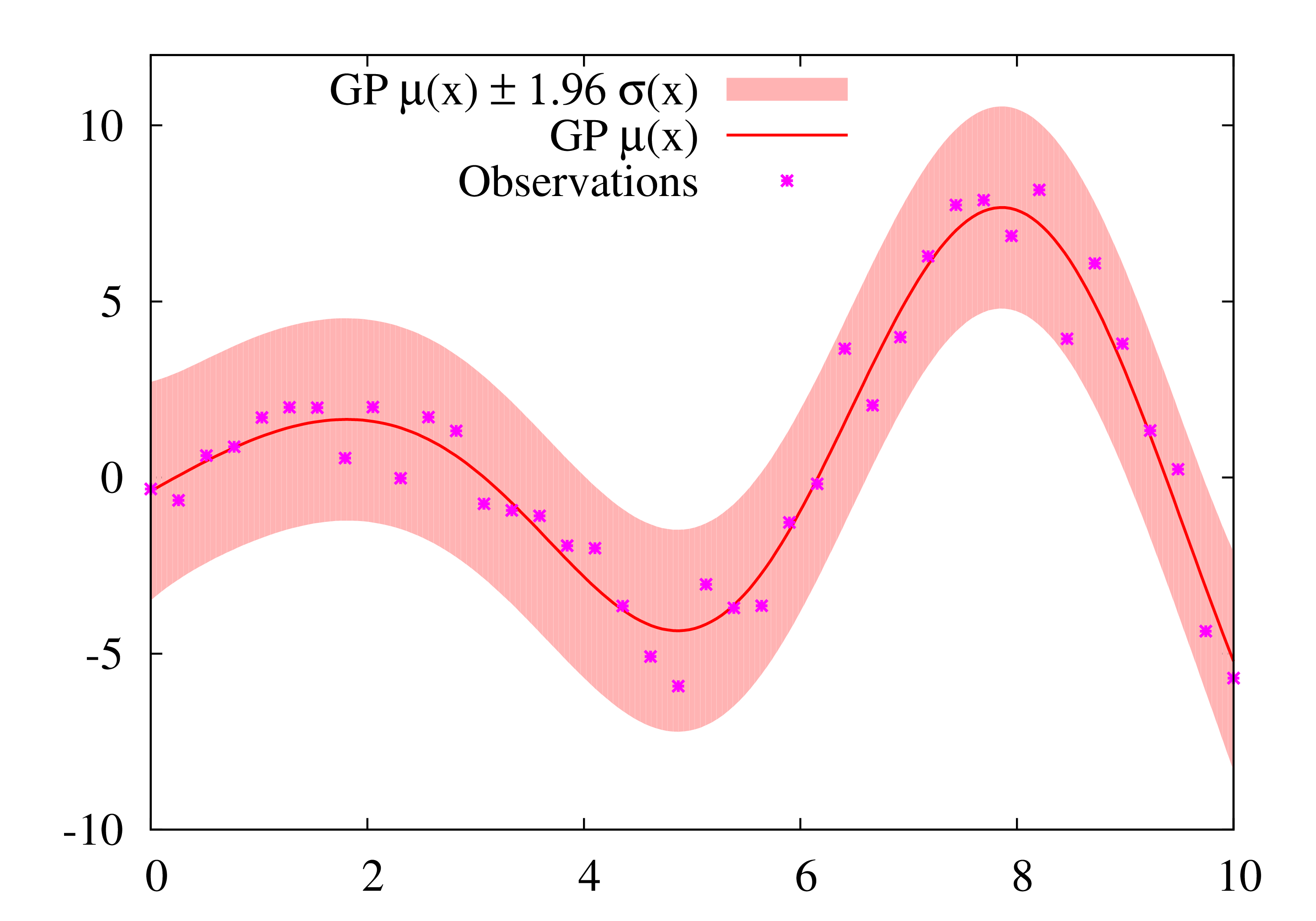
高斯过程被认为是一种机器学习算法,是以惰性学习|lazy learning方式,利用点与点之间同质性的度量作为核函数|Kernel function,以从输入的训练数据预测未知点的值。其预测结果不仅包含该点的值,而同时包含不确定性的资料-它的一维高斯分布(即该点的边际分布)。
对于某些核函数,可以使用矩阵代数(见克里金插值法|kriging条目)来计算预测值。若核函数有代数参数,则通常使用软体以拟合高斯过程的模型。
由于高斯过程是基于高斯分布(正态分布)的概念,故其以卡尔•弗里德里希•高斯为名。可以把高斯过程看成多元正态分布的无限维广义延伸。
高斯过程常用于统计建模中,而使用高斯过程的模型可以得到高斯过程的属性。举例来说,如果把一随机过程用高斯过程建模,我们可以显示求出各种导出量的分布,这些导出量可以是例如随机过程在一定范围次数内的平均值,及使用小范围采样次数及采样值进行平均值预测的误差。
目录
定义
一统计学分布定义为{Xt, t∈T}是一个高斯过程,当且仅当对下标集合T的任意有限子集t1,...,tk,
X_{t_1, \ldots, t_k} = (X_{t_1}, \ldots, X_{t_k})
是一个多元正态分布,这等同于说(X_{t_1}, \ldots, X_{t_k})的任一线性组合是一单变量正态分布。更准确地,取样函数Xt 的任一线性泛函均会得出正态分布。可以写成X ~ GP(m,K),即随机函数X 以高斯过程(GP)方式分布,且其平均数函数为m 及其协方差函数为K。当输入向量t为二维或多维时,高斯过程亦可能被称为高斯自由场(高斯场|Gaussian random field)。
协方差函数
高斯过程的关键事实是它们可以完全由它们的二阶统计量来定义.因此,如果高斯过程被假定为具有平均值零, defining 协方差函数完全定义了过程的行为。重要的是,这个函数的非负定性使得它的谱分解使用了 K-L转换.
可以通过协方差函数定义的基本方面是过程的平稳过程, 各向同性, 光滑函数 和 周期函数。
平稳过程指的是过程的任何两点x和x'的分离行为。如果过程是静止的,取决于它们的分离x-x',而如果非平稳则取决于x和x'的实际位置。例如,一个特例 Ornstein–Uhlenbeck process|Ornstein–Uhlenbeck 过程, 一个 布朗运动 过程,是固定的。
如果过程仅依赖于 |x-x'|,x和x'之间的欧几里德距离(不是方向),那么这个过程被认为是各向同性的。同时存在静止和各向同性的过程被认为是 同质与异质;在实践中,这些属性反映了在给定观察者位置的过程的行为中的差异(或者更确切地说,缺乏这些差异)。
最终高斯过程翻译为功能先验,这些先验的平滑性可以由协方差函数引起。如果我们预期对于“接近”的输入点x和x',其相应的输出点y和y'也是“接近”,则存在连续性的假设。如果我们希望允许显著的位移,那么我们可以选择一个更粗糙的协方差函数。行为的极端例子是Ornstein-Uhlenbeck协方差函数和前者不可微分和后者无限可微的平方指数。 周期性是指在过程的行为中引发周期性模式。形式上,这是通过将输入x映射到二维向量u(x) = (\cos(x), \sin(x)) 来实现的。
常见的协方差函数
一些常见的协方差函数:
- 常值: K_\operatorname{C}(x,x') = C
- 线性: K_\operatorname{L}(x,x') = x^T x'
- 高斯噪声: K_\operatorname{GN}(x,x') = \sigma^2 \delta_{x,x'}
- 平方指数: K_\operatorname{SE}(x,x') = \exp \Big(-\frac{\|d\|^2}{2\ell^2} \Big)
- Ornstein–Uhlenbeck : K_\operatorname{OU}(x,x') = \exp \left(-\frac{|d|} \ell \right)
- Matérn: K_\operatorname{Matern}(x,x') = \frac{2^{1-\nu}}{\Gamma(\nu)} \Big(\frac{\sqrt{2\nu}|d|}{\ell} \Big)^\nu K_\nu \Big(\frac{\sqrt{2\nu}|d|}{\ell} \Big)
- 定期: K_\operatorname{P}(x,x') = \exp\left(-\frac{ 2\sin^2\left(\frac d 2 \right)}{\ell^2} \right)
- 有理二次方: K_\operatorname{RQ}(x,x') = (1+|d|^2)^{-\alpha}, \quad \alpha \geq 0