一次函数查看源代码讨论查看历史
| 一次函数 |
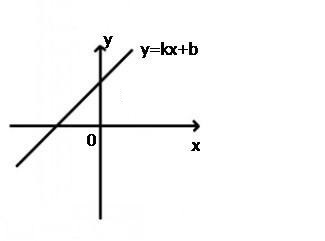 |
一次函数,在某一个变化过程中,设有两个变量x和y,如果满足这样的关系:y=kx+b(k为一次项系数且k≠0,b为任意常数,),那么我们就说y是x的一次函数,其中x是自变量,y是因变量 (又称函数)。
简介
1.求函数图像的k值(斜率):(y1-y2)/(x1-x2);
2.求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2];
3.两点距离的平方的公式:[(x1-x2)^2+(y1-y2)^2 ];
4.求任意两点的连线的一次函数解析式:(y-y1)/(x-x1)=(y2-y1)/(x2-x1) 。
5.直线y=kx+b交x轴于点(-b/k,0), 交y轴于点(0,b);
6.求两个一次函数式图像交点坐标:解两函数式
两个一次函数 y1=k1x+b1,y2=k2x+b2,令y1=y2,得k1x+b1=k2x+b2。将解得的x=x0值代回y1=k1x+b1或y2=k2x+b2两式的任一式,得到y=y0,则(x0, y0)即为 y1=k1x+b1与y2=k2x+b2的交点坐标。
7.求任意两点的连线的一次函数解析式:(y-y1)/(x-x1)=(y2-y1)/(x2-x1) (若分母为0,则分子为0)
(x,y)的正负性为 +,+(正,正)时该点在第一象限
(x,y)的正负性为 -,+(负,正)时该点在第二象限
(x,y)的正负性为 - ,-(负,负)时该点在第三象限
(x,y)的正负性为 +,-(正,负)时该点在第四象限
8.若两条直线y1=k1x+b1,y2=k2x+b2互相平行,则k1=k2,b1≠b2
9.如两条直线y1=k1x+b1,y2=k2x+b2互相垂直,则k1*k2=-1
10.设原直线为y=f(x)=kx+b
y‘=f(x-n)=k(x-n)+b就是原直线图像向右平移n个单位,
y’=f(x+n)=k(x+n)+b就是原直线图像向左平移n个单位,
y’=f(x)+n=kx+b+n就是原直线图像向上平移n个单位,
y’=f(x)-n=kx+b-n就是原直线图像向下平移n个单位。
口诀:左加右减相对于X,上加下减相对于Y。
评价
“函数”一词最初是由德国的数学家莱布尼茨在17世纪采用的,当时莱布尼茨用“函数”这一词来表示变量x的幂,即x2,x3,….接下来莱布尼茨又将“函数”这一词用来表示曲线上的横坐标、纵坐标、切线的长度、垂线的长度等等所有与曲线上的点有关的变量.就这样“函数”这词逐渐盛行.
在中国,古时候的人将“函”字与“含”字通用,都有着“包含”的意思,清代数学家、天文学家、翻译家和教育家,近代科学的先驱者李善兰给出的定义是:“凡式中含天,为天之函数.”中国的古代人还用“天、地、人、物”4个字来表示4个不同的未知数或变量,显然,在李善兰的这个定义中的含义就是“凡是公式中含有变量x,则该式子叫做x的函数.”这样,在中国“函数”是指公式里含有变量的意思.
瑞士数学家雅克·柏努意给出了和莱布尼茨相同的函数定义.1718年,雅克·柏努意的弟弟约翰·柏努意给出了函数了如下的定义:由任一变数和常数的任意形式所构成的量叫做这一变数的函数.换句话说,由x和常量所构成的任一式子都可称之为关于x的函数.
1775年,欧拉把函数定义为:“如果某些变量:以某一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随着变化,我们把前面的变量称为后面变量的函数.”由此可以看到,由莱布尼兹到欧拉所引入的函数概念,都还是和解析表达式、曲线表达式等概念纠缠在一起.
首屈一指的法国数学家柯西引入了新的函数定义:“在某些变数间存在着一定的关系,当一经给定其中某一变数的值,其它变数的值也可随之而确定时,则将最初的变数称之为‘自变量’,其它各变数则称为‘函数’”.在柯西的定义中,首先出现了“自变量”一词.
1834年,俄国数学家罗巴契夫斯基进一步提出函数的定义:“x的函数是这样的一个数,它对于每一个x都有确定的值,并且随着x一起变化.函数值可以由解析式给出,也可以由一个条件给出,这个条件提供了一种寻求全部对应值的方法.函数的这种依赖关系可以存在,但仍然是未知的”.这个定义指出了对应关系。即条件的必要性,利用这个关系以求出每一个x的对应值.
1837年德国数学家狄里克雷认为怎样去建立x与y之间的对应关系是无关紧要的,所以他的定义是:“如果对于x的每一个值,y总有一个完全确定的值与之对应,则y是x的函数.”
德国数学家黎曼引入了函数的新定义:“对于x的每一个值,y总有完全确定了的值与之对应,而不拘建立x,y之间的对应方法如何,均将y称为x的函数.”
上面函数概念的演变,我们可以知道,函数的定义必须抓住函数的本质属性,变量y称为x的函数,只须有一个法则存在,使得这个函数取值范围中的每一个值,有一个确定的y值和它对应就行了,不管这个法则是公式或图象或表格或其他形式。[1]