一次函數
| 一次函數 |
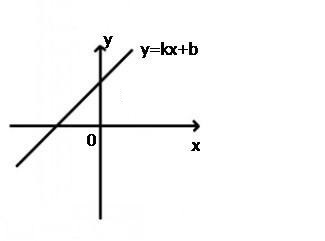 |
一次函數,在某一個變化過程中,設有兩個變量x和y,如果滿足這樣的關係:y=kx+b(k為一次項係數且k≠0,b為任意常數,),那麼我們就說y是x的一次函數,其中x是自變量,y是因變量 (又稱函數)。
簡介
1.求函數圖像的k值(斜率):(y1-y2)/(x1-x2);
2.求任意2點所連線段的中點坐標:[(x1+x2)/2,(y1+y2)/2];
3.兩點距離的平方的公式:[(x1-x2)^2+(y1-y2)^2 ];
4.求任意兩點的連線的一次函數解析式:(y-y1)/(x-x1)=(y2-y1)/(x2-x1) 。
5.直線y=kx+b交x軸於點(-b/k,0), 交y軸於點(0,b);
6.求兩個一次函數式圖像交點坐標:解兩函數式
兩個一次函數 y1=k1x+b1,y2=k2x+b2,令y1=y2,得k1x+b1=k2x+b2。將解得的x=x0值代回y1=k1x+b1或y2=k2x+b2兩式的任一式,得到y=y0,則(x0, y0)即為 y1=k1x+b1與y2=k2x+b2的交點坐標。
7.求任意兩點的連線的一次函數解析式:(y-y1)/(x-x1)=(y2-y1)/(x2-x1) (若分母為0,則分子為0)
(x,y)的正負性為 +,+(正,正)時該點在第一象限
(x,y)的正負性為 -,+(負,正)時該點在第二象限
(x,y)的正負性為 - ,-(負,負)時該點在第三象限
(x,y)的正負性為 +,-(正,負)時該點在第四象限
8.若兩條直線y1=k1x+b1,y2=k2x+b2互相平行,則k1=k2,b1≠b2
9.如兩條直線y1=k1x+b1,y2=k2x+b2互相垂直,則k1*k2=-1
10.設原直線為y=f(x)=kx+b
y『=f(x-n)=k(x-n)+b就是原直線圖像向右平移n個單位,
y』=f(x+n)=k(x+n)+b就是原直線圖像向左平移n個單位,
y』=f(x)+n=kx+b+n就是原直線圖像向上平移n個單位,
y』=f(x)-n=kx+b-n就是原直線圖像向下平移n個單位。
口訣:左加右減相對於X,上加下減相對於Y。
評價
「函數」一詞最初是由德國的數學家萊布尼茨在17世紀採用的,當時萊布尼茨用「函數」這一詞來表示變量x的冪,即x2,x3,….接下來萊布尼茨又將「函數」這一詞用來表示曲線上的橫坐標、縱坐標、切線的長度、垂線的長度等等所有與曲線上的點有關的變量.就這樣「函數」這詞逐漸盛行.
在中國,古時候的人將「函」字與「含」字通用,都有着「包含」的意思,清代數學家、天文學家、翻譯家和教育家,近代科學的先驅者李善蘭給出的定義是:「凡式中含天,為天之函數.」中國的古代人還用「天、地、人、物」4個字來表示4個不同的未知數或變量,顯然,在李善蘭的這個定義中的含義就是「凡是公式中含有變量x,則該式子叫做x的函數.」這樣,在中國「函數」是指公式里含有變量的意思.
瑞士數學家雅克·柏努意給出了和萊布尼茨相同的函數定義.1718年,雅克·柏努意的弟弟約翰·柏努意給出了函數了如下的定義:由任一變數和常數的任意形式所構成的量叫做這一變數的函數.換句話說,由x和常量所構成的任一式子都可稱之為關於x的函數.
1775年,歐拉把函數定義為:「如果某些變量:以某一種方式依賴於另一些變量,即當後面這些變量變化時,前面這些變量也隨着變化,我們把前面的變量稱為後面變量的函數.」由此可以看到,由萊布尼茲到歐拉所引入的函數概念,都還是和解析表達式、曲線表達式等概念糾纏在一起.
首屈一指的法國數學家柯西引入了新的函數定義:「在某些變數間存在着一定的關係,當一經給定其中某一變數的值,其它變數的值也可隨之而確定時,則將最初的變數稱之為『自變量』,其它各變數則稱為『函數』」.在柯西的定義中,首先出現了「自變量」一詞.
1834年,俄國數學家羅巴契夫斯基進一步提出函數的定義:「x的函數是這樣的一個數,它對於每一個x都有確定的值,並且隨着x一起變化.函數值可以由解析式給出,也可以由一個條件給出,這個條件提供了一種尋求全部對應值的方法.函數的這種依賴關係可以存在,但仍然是未知的」.這個定義指出了對應關係。即條件的必要性,利用這個關係以求出每一個x的對應值.
1837年德國數學家狄里克雷認為怎樣去建立x與y之間的對應關係是無關緊要的,所以他的定義是:「如果對於x的每一個值,y總有一個完全確定的值與之對應,則y是x的函數.」
德國數學家黎曼引入了函數的新定義:「對於x的每一個值,y總有完全確定了的值與之對應,而不拘建立x,y之間的對應方法如何,均將y稱為x的函數.」
上面函數概念的演變,我們可以知道,函數的定義必須抓住函數的本質屬性,變量y稱為x的函數,只須有一個法則存在,使得這個函數取值範圍中的每一個值,有一個確定的y值和它對應就行了,不管這個法則是公式或圖象或表格或其他形式。[1]