高斯過程檢視原始碼討論檢視歷史
 |
在概率論[1] 和統計學中,高斯過程(Gaussian process)是觀測值出現在一個連續域(例如時間或空間)的隨機過程。在高斯過程中,連續輸入空間中每個點都是與一個正態分布的隨機變量相關聯。此外,這些隨機變量的每個有限集合都有一個多元正態分布,換句話說他們的任意有限線性組合是一個正態分布。高斯過程的分布是所有那些(無限多個)隨機變量的聯合分布,正因如此,它是連續域(例如時間或空間)上函數的分布。
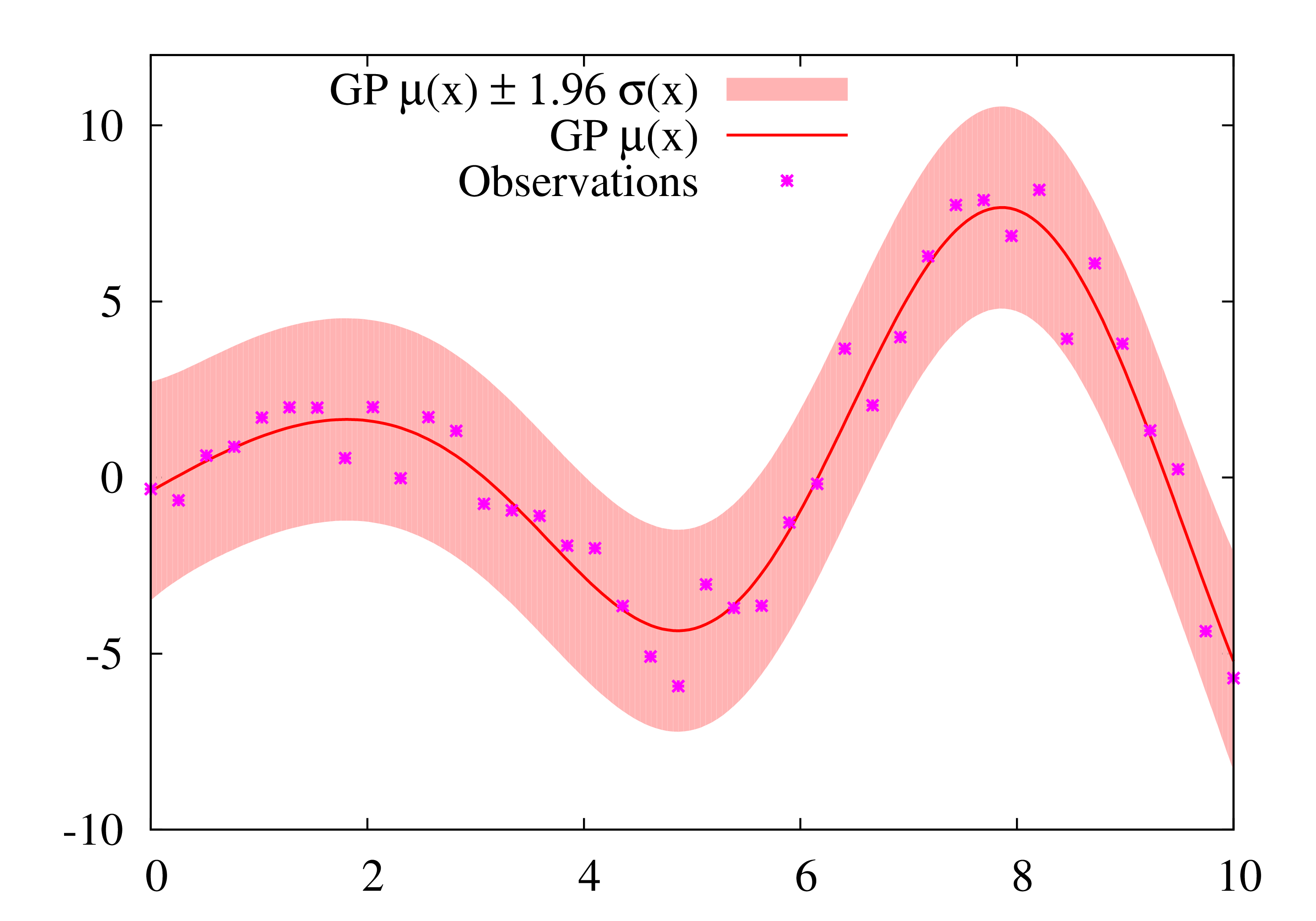
高斯過程被認為是一種機器學習算法,是以惰性學習|lazy learning方式,利用點與點之間同質性的度量作為核函數|Kernel function,以從輸入的訓練數據預測未知點的值。其預測結果不僅包含該點的值,而同時包含不確定性的資料-它的一維高斯分佈(即該點的邊際分佈)。
對於某些核函數,可以使用矩陣代數(見克里金插值法|kriging條目)來計算預測值。若核函數有代數參數,則通常使用軟體以擬合高斯過程的模型。
由於高斯過程是基於高斯分佈(正態分佈)的概念,故其以卡爾•弗里德里希•高斯為名。可以把高斯過程看成多元正態分佈的無限維廣義延伸。
高斯過程常用於統計建模中,而使用高斯過程的模型可以得到高斯過程的屬性。舉例來說,如果把一隨機過程用高斯過程建模,我們可以顯示求出各種導出量的分布,這些導出量可以是例如隨機過程在一定範圍次數內的平均值,及使用小範圍採樣次數及採樣值進行平均值預測的誤差。
定義
一統計學分佈定義為{Xt, t∈T}是一個高斯過程,當且僅當對下標集合T的任意有限子集t1,...,tk,
X_{t_1, \ldots, t_k} = (X_{t_1}, \ldots, X_{t_k})
是一個多元正態分布,這等同於說(X_{t_1}, \ldots, X_{t_k})的任一線性組合是一單變量正態分佈。更準確地,取樣函數Xt 的任一線性泛函均會得出正態分佈。可以寫成X ~ GP(m,K),即隨機函數X 以高斯過程(GP)方式分佈,且其平均數函數為m 及其協方差函數為K。當輸入向量t為二維或多維時,高斯過程亦可能被稱為高斯自由場(高斯場|Gaussian random field)。
有些人假設隨機變量 Xt 平均為0;其可以在不失一般性的前提下簡化運算,且高斯過程的均方屬性可完全由協方差函數K得出。
協方差函數
高斯過程的關鍵事實是它們可以完全由它們的二階統計量來定義.因此,如果高斯過程被假定為具有平均值零, defining 協方差函數完全定義了過程的行為。重要的是,這個函數的非負定性使得它的譜分解使用了 K-L轉換.
可以通過協方差函數定義的基本方面是過程的平穩過程, 各向同性, 光滑函數 和 週期函數。
平穩過程指的是過程的任何兩點x和x'的分離行為。如果過程是靜止的,取決於它們的分離x-x',而如果非平穩則取決於x和x'的實際位置。例如,一個特例 Ornstein–Uhlenbeck process|Ornstein–Uhlenbeck 過程, 一個 布朗運動 過程,是固定的。
如果過程僅依賴於 |x-x'|,x和x'之間的歐幾里德距離(不是方向),那麼這個過程被認為是各向同性的。同時存在靜止和各向同性的過程被認為是 同質與異質;在實踐中,這些屬性反映了在給定觀察者位置的過程的行為中的差異(或者更確切地說,缺乏這些差異)。
最終高斯過程翻譯為功能先驗,這些先驗的平滑性可以由協方差函數引起。如果我們預期對於「接近」的輸入點x和x',其相應的輸出點y和y'也是「接近」,則存在連續性的假設。如果我們希望允許顯著的位移,那麼我們可以選擇一個更粗糙的協方差函數。行為的極端例子是Ornstein-Uhlenbeck協方差函數和前者不可微分和後者無限可微的平方指數。 週期性是指在過程的行為中引發週期性模式。形式上,這是通過將輸入x映射到二維向量u(x) = (\cos(x), \sin(x)) 來實現的。
常見的協方差函數
一些常見的協方差函數:
- 常值: K_\operatorname{C}(x,x') = C
- 線性: K_\operatorname{L}(x,x') = x^T x'
- 高斯噪聲: K_\operatorname{GN}(x,x') = \sigma^2 \delta_{x,x'}
- 平方指數: K_\operatorname{SE}(x,x') = \exp \Big(-\frac{\|d\|^2}{2\ell^2} \Big)
- Ornstein–Uhlenbeck : K_\operatorname{OU}(x,x') = \exp \left(-\frac{|d|} \ell \right)
- Matérn: K_\operatorname{Matern}(x,x') = \frac{2^{1-\nu}}{\Gamma(\nu)} \Big(\frac{\sqrt{2\nu}|d|}{\ell} \Big)^\nu K_\nu \Big(\frac{\sqrt{2\nu}|d|}{\ell} \Big)
- 定期: K_\operatorname{P}(x,x') = \exp\left(-\frac{ 2\sin^2\left(\frac d 2 \right)}{\ell^2} \right)
- 有理二次方: K_\operatorname{RQ}(x,x') = (1+|d|^2)^{-\alpha}, \quad \alpha \geq 0