複利檢視原始碼討論檢視歷史
| 複利 |
 |
|
中文名: 複利 別稱: 利滾利;以利生利 應用學科: 經濟學;金融學 |
複利,Compound interest,是一種計算利息的方法。按照這種方法,利息除了會根據本金計算外,新得到的利息同樣可以生息,因此俗稱「利滾利」、「驢打滾」或「利疊利」。只要計算利息的周期越密,財富增長越快,而隨着年期越長,複利效應也會越來越明顯。[1]
基本概念
複利,復是與單利相對應的經濟概念,單利的計算不用把利息計入本金,而複利恰恰相反,它的利息要併入本金中重複計息。複利就是複合利息,它是指每年的收益還可以產生收益,具體是將整個借貸期限分割為若干段,前一段按本金計算出的利息要加入到本金中,形成增大了的本金,作為下一段計算利息的本金基數,直到每一段的利息都計算出來,加總之後,就得出整個借貸期內的利息,簡單來說就是俗稱的利滾利。愛因斯坦稱其為「世界第八大奇觀」。
公式
複利的計算是對本金及其產生的利息一併計算,也就是利上有利。
複利計算的特點是:把上期末的本利和作為下一期的本金,在計算時每一期本金的數額是不同的。複利的計算公式是:
複利現值是指在計算複利的情況下,要達到未來某一特定的資金金額,現今必須投入的本金。 所謂複利也稱利上加利,是指一筆存款或者投資獲得回報之後,再連本帶利進行新一輪投資的方法。
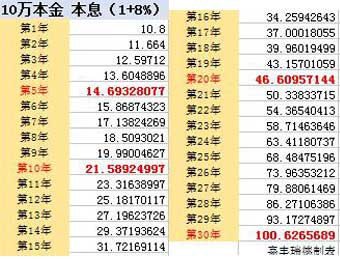
複利終值是指本金在約定的期限內獲得利息後,將利息加入本金再計利息,逐期滾算到約定期末的本金之和。簡單來講,就是在期初存入A,以i為利率,存n期後的本金與利息之和。公式:F=A*(1+i)^n.
例如:本金為50000元,利率或者投資回報率為3%,投資年限為30年,那麼,30年後所獲得的利息收入,按複利計算公式來計算本利和(終值)是:50000×(1+3%)^30
由於,通脹率和利率密切關聯,就像是一個硬幣的正反兩面,所以,複利終值的計算公式也可以用以計算某一特定資金在不同年份的實際價值。只需將公式中的利率換成通脹率即可。
計算意義
複利計算的特點是:把上期未的本利和作為下一期的本金,在計算時每一期本金的數額是不同的。複利的計算公式是:S = P(I + i)^n,其中以符號I代表利息,P代表本金,n代表時期,i代表利率,S代表本利和。
複利的報酬驚人,比方說拿10萬元去買年報酬率20%的股票,大約3年半的時間,10萬元就變成20萬元。複利的時間乘數效果,更是這其中的奧妙所在。複利的力量是巨大的,印度有個古老故事,國王與象棋國手下棋輸了,國手要求在第一個棋格中放上一粒麥子,第二格放上兩粒,第三格放上四粒,以此類推即按複利增長的方式放滿整個棋格。國王以為這個棋手可以得到一袋麥子,結果卻是全印度的麥子都不足以支付。 所以,追逐複利的力量,正是資本積累的動力。