滑模控制檢視原始碼討論檢視歷史

滑模控制

來自 X技術

中文名：滑模控制 外文名：sliding mode control 別 名：變結構控制 本 質：特殊的非線性控制

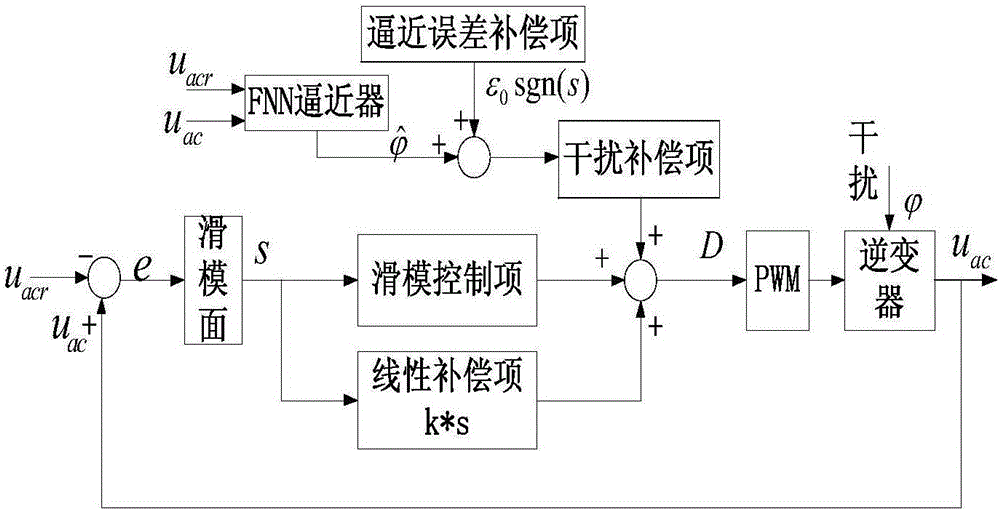
滑模控制(sliding mode control, SMC)也叫變結構控制，本質上是一類特殊的非線性控制，且非線性表現為控制的不連續性。這種控制策略與其他控制的不同之處在於系統的「結構」並不固定，而是可以在動態過程中，根據系統當前的狀態（如偏差及其各階導數等）有目的地不斷變化，迫使系統按照預定「滑動模態」的狀態軌跡運動。由於滑動模態可以進行設計且與對象參數及擾動無關，這就使得滑模控制具有快速響應、對應參數變化及擾動不靈敏、無需系統在線辨識、物理實現簡單等優點。

簡述

20世紀50年代前蘇聯學者提出變結構控制，變結構控制起源於繼電器控制和 Bang-Bang 控制，它與常規控制的區別在於控制的不連續性。滑模控制是變結構控制的一 個分支。它是一種非線性控制，通過切換函數來實現，根據系統狀態偏離滑模的程度來切換控制器的結構（控制律或控制器參數），從而使系統按照滑模規定的規律運行的控制方法。滑模控制已形成一套比較完整的理論體系，並已廣泛應用到各種工業控制對象之中。滑模控制得到廣泛應用的主要原因是，對非線性系統的良好控制性能，對多輸入多輸出系統的可應用性，對離散時間系統的建立良好的設計標準。滑模控制的重要的優點是魯棒性，當系統處於滑動模型，對被控對象的模型誤差、對象參數的變化以及外部干擾有極佳的不敏感性。

原理

滑模變結構控制的原理，是根據系統所期望的動態特性來設計系統的切換超平面，通過滑動模態控制器使系統狀態從超平面之外向切換超平面收束。系統一旦到達切換超平面，控制作用將保證系統沿切換超平面到達系統原點，這一沿切換超平面向原點滑動的過程稱為滑模控制。由於系統的特性和參數只取決於設計的切換超平面而與外界干擾沒有關係，所以滑模變結構控制具有很強的魯棒性。超平面的設計方法有極點配置，特徵向量配置設計法，最優化設計方法等，所設計的切換超平面需滿足達到條件，即系統在滑模平面後將保持在該平面的條件。控制器的設計有固定順序控制器設計、自由順序控制器設計和最終滑動控制器設計等設計方法[1]。以N維狀態空間模型為例，採用極點配置方法得到M(N<M)維切換超平面，控制器採用固定順序控制器的設計方式，首先控制器控制任意點到Q1超平面（M維）形成M-1階滑動模態，系統到達Q1超平面後由於該平面的達到條件而保持在該超平面上所以後面的超平面將是該超平面的子集；然後控制器採用Q1對應的控制規則驅動到Q1與Q2交接的Q12平面（M-1維）得到M-2滑動模態，然後在Q12對應的控制規則驅動下到Q12與Q3交接的Q123平面（M-2維），依次到Q123.m平面，得到最終的滑模，系統在將在達到條件下保持在該平面，使系統得到期望的性能。

優點

滑模控制的優點是能夠克服系統的不確定性, 對干擾和未建模動態具有很強的魯棒性，尤其是對非線性系統的控制具有良好的控制效果。由於變結構控制系統算法簡單，響應速度快，對外界噪聲干擾和參數攝動具有魯棒性，在機器人控制領域得到了廣泛的應用，也有學者將滑模變結構方法應用於空間機器人控制。變結構控制作為非線性控制的重要方法近年來得到了廣泛深入的研究，其中一個重要的研究分支是抑制切換振顫，這方面已取得了不小的進展，提出了等效控制、 切換控制與模糊控制的組合模糊調整控制方法，其中等效控制用來配置極點，切換控制用來保證不確定外擾存在下的到達過程，模糊調整控制則用來提高控制性能並減少振顫。研究了一類非線性系統的模糊滑模變結構控制方法，設計了滑模控制器和 PI控制器的組合模糊邏輯控制器，充分發揮了各控制器的優點。提出了基於有限時間機理的快速 Terminal 滑模控制方法並給出了與普通 Terminal 滑模控制性能的比較。設計了針對參數不確定與外干擾的非奇異 Teminal 滑模控制方法，並提出了分等級控制結構以簡化控制器設計。上述這些方法在實際系統中雖然得到了有效應用，但無論是自適應滑模控制還是模糊神經網絡控制，均增加了系統複雜性與物理實現難度。顯然，尋找具有良好效能並易於實現的控制。

缺點

滑模控制的缺點：當狀態軌跡到達滑動模態面後，難以嚴格沿着滑動模態面向平衡點滑動，而是在其兩側來回穿越地趨近平衡點，從而產生抖振——滑模控制實際應用中的主要障礙。

設計步驟

在系統控制過程中，控制器根據系統當時狀態，以躍變方式有目的地不斷變換，迫使系統按預定的「 滑動模態」 的狀態軌跡運動。變結構是通過切換函數實現的，特別要指出的是，通常要求切換面上存在滑動模態區，故變結構控制又常被稱為滑動模態控制。設計變結構控制系統基本可分為兩步：

確定切換函數 S ( x)

即開關面，使它所確定的滑動模態漸近穩定且有良好的品質，開關面代表了系統的理想動態特性。

設計滑模控制器，使到達條件得到滿足，從而使趨近運動 (非滑動模態 )於有限時間到達開關面，並且在趨近的過程中快速、 抖振小。

特點

在普通的滑模控制中 ,通常選擇一個線性的滑動超平面，使系統到達滑動模態後，跟蹤誤差漸進地收斂為零，並且收斂的速度可以通過選擇滑模面參數矩陣來調節。但理論上講，無論如何狀態跟蹤誤差都不會在有限的時間內收斂為零。Ter minal滑模控制是通過設計一種動態非線性滑模面方程實現的，即在保證滑模控制穩定性的基礎上，使系統狀態在指定的有限時間內達到對期望狀態的完全跟蹤。將動態非線性滑模面方程設計為 s = x2 +βxq/ p1 。但該控制方法由於非線性函數的引入使得控制器在實際工程中實現困難，而且如果參數選取不當，還會出現奇異問題。對一個二階系統給出了相應的 Terminal滑面，滑模面的導數是不連續的，不適用於高階系統。莊開宇等設計了一種用於高階非線性系統的 Terminal滑面，克服了滑模面中導數不連續的缺點，並消除了滑模控制的到達階段，確保了系統的全局魯棒性和穩定性。

重要意義

近年來，滑模變結構方法因其所具有的優良特性而受到越來越多的重視。該方法通過自行設計所需的滑模面和等效控制律，能快速響應輸入的變換，而對參數變換和擾動不敏感，具有很好的魯棒性，且物理製作簡單。大多數採用滑模變結構方法的控制系統沒採用聯合滑模觀測和滑模控制的思想進行魯棒方案的設計。滑模變結構控制逐漸引起了學者們的重視，其最大優點是滑動模態對加在系統上的干擾和系統的攝動具有完全的自適應性，而且系統狀態一旦進入滑模運動，便快速地收斂到控制目標，為時滯系統、不確定性系統的魯棒性設計提供了一種有效途徑，但其最大的問題是系統控制器的輸出具有抖動。

互聯網滑模控制系統