常态分布查看源代码讨论查看历史
 |
常态分布(normal distribution)又名高斯分布(Gaussian distribution),是一个非常常见的连续机率分布[1] 。常态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。
若随机变量<math>X</math>服从一个位置参数为mu、尺度参数为sigma的常态分布,记为:
- X \sim N(\mu,\sigma^2)
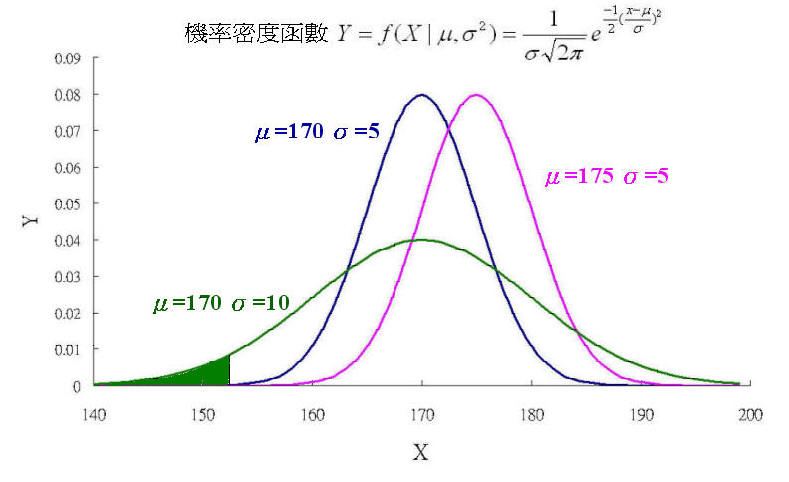
则其机率密度函数为 f(x) = \frac1{\sigma\sqrt{2\pi}}\; e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2} }
常态分布的数学期望值或期望值<math>\mu</math>等于位置参数,决定了分布的位置;其方差<math>\sigma^2</math>的开平方或标准差<math>\sigma</math>等于尺度参数,决定了分布的幅度。
常态分布的机率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此得名)。我们通常所说的标准常态分布是位置参数mu = 0,尺度参数sigma^2 = 1的常态分布。
概要
常态分布是自然科学与行为科学中的定量现象的一个方便模型。各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从常态分布。尽管这些现象的根本原因经常是未知的,理论上可以证明如果把许多小作用加起来看做一个变量,那么这个变量服从常态分布(在R.N.Bracewell的Fourier transform and its application中可以找到一种简单的证明)。常态分布出现在许多区域统计:例如,采样分布均值是近似地常态的,即使被采样的样本的原始群体分布并不服从常态分布。另外,常态分布信息熵在所有的已知均值及方差的分布中最大,这使得它作为一种均值以及方差已知的分布的自然选择。常态分布是在统计以及许多统计测试中最广泛应用的一类分布。在概率论,常态分布是几种连续以及离散分布的极限分布。
历史
常态分布最早是棣莫弗在1718年著作的书籍的(Doctrine of Change),及1734年发表的一篇关于二项分布文章中提出的,当二项随机变数的位置参数n很大及形状参数p为1/2时,则所推导出二项分布的近似分布函数就是常态分布。拉普拉斯在1812年发表的《分析概率论》(Theorie Analytique des Probabilites)中对棣莫佛的结论作了扩展到二项分布的位置参数为n及形状参数为1>p>0时。现在这一结论通常被称为棣莫佛-拉普拉斯定理。
拉普拉斯在误差分析试验中使用了常态分布。勒让德于1805年引入最小二乘法这一重要方法;而高斯则宣称他早在1794年就使用了该方法,并通过假设误差服从常态分布给出了严格的证明。
“钟形曲线”这个名字可以追溯到Jouffret他在1872年首次提出这个术语“钟形曲面”,用来指代二元常态分布(bivariate normal)。正态分布这个名字还被Charles S. Peirce、Francis Galton、Wilhelm Lexis在1875分别独立地使用。这个术语是不幸的,因为它反映和鼓励了一种谬误,即很多概率分布都是常态的。(请参考下面的“实例”)
这个分布被称为“常态”或者“高斯”正好是Stigler名字由来法则的一个例子,这个法则说“没有科学发现是以它最初的发现者命名的”。
正态分布的定义
有几种不同的方法用来说明一个随机变量。最直观的方法是概率密度函数,这种方法能够表示随机变量每个取值有多大的可能性。累积分布函数是一种概率上更加清楚的方法,请看下边的例子。还有一些其他的等价方法,例如cumulant、特征函数、动差生成函数以及cumulant-生成函数。这些方法中有一些对于理论工作非常有用,但是不够直观。请参考关于概率分布的讨论。
概率密度函数
常态分布的概率密度函数均值为mu 方差为sigma^2 (或标准差sigma)是高斯函数的一个实例:
- f(x;\mu,\sigma)
frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)。
如果一个随机变量X服从这个分布,我们写作 X ~ N(\mu, \sigma^2). 如果mu = 0并且sigma = 1,这个分布被称为标准正态分布,这个分布能够简化为
- f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right)。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
- 平均值与它的众数(statistical mode)以及中位数(median)同一数值。
- 函数曲线下68.268949%的面积在平均数左右的一个标准差范围内。
- 95.449974%的面积在平均数左右两个标准差2 \sigma的范围内。
- 99.730020%的面积在平均数左右三个标准差3 \sigma的范围内。
- 99.993666%的面积在平均数左右四个标准差4 \sigma的范围内。
- 函数曲线的拐点(inflection point)为离平均数一个标准差距离的位置。
性质
常态分布的一些性质:
- 如果X \sim N(\mu, \sigma^2) 且a与b是实数,那么a X + b \sim N(a \mu + b, (a \sigma)^2).
- 如果X \sim N(\mu_X, \sigma^2_X)与Y \sim N(\mu_Y, \sigma^2_Y)是统计独立的常态随机变量,那么:
- 它们的和也满足常态分布U = X + Y \sim N(\mu_X + \mu_Y, \sigma^2_X + \sigma^2_Y) (正态分布随机变量总和|sum of normally distributed random variables|proof).
- 它们的差也满足常态分布V = X - Y \sim N(\mu_X - \mu_Y, \sigma^2_X + \sigma^2_Y).
- U与V两者是相互独立的。(要求X与Y的方差相等)
- 如果X \sim N(0, \sigma^2_X)和Y \sim N(0, \sigma^2_Y)是独立常态随机变量,那么:
- 它们的积X Y服从机率密度函数为p的分布
- p(z) = \frac{1}{\pi\,\sigma_X\,\sigma_Y} \; K_0\left(\frac{|z|}{\sigma_X\,\sigma_Y}\right),其中K_0是修正贝塞尔函数(modified Bessel function)
- 它们的比符合柯西分布,满足X/Y \sim \mathrm{Cauchy}(0, \sigma_X/\sigma_Y).
- 它们的积X Y服从机率密度函数为p的分布
- 如果X_1, \cdots, X_n为独立标准常态随机变量,那么X_1^2 + \cdots + X_n^2服从自由度为n的卡方分布。
中心极限定理
常态分布有一个非常重要的性质:在特定条件下,大量统计独立的随机变量的平均值的分布趋于正态分布,这就是中心极限定理。中心极限定理的重要意义在于,根据这一定理的结论,其他概率分布可以用正态分布作为近似。
- 参数为n和p的二项分布,在n相当大而且p接近0.5时近似于正态分布。
近似正态分布平均数为mu = n p且方差为sigma^2 = n p (1 - p).
- 一泊松分布带有参数lambda当取样样本数很大时将近似正态分布lambda.
近似正态分布平均数为mu = \lambda且方差为sigma^2 = \lambda.
这些近似值是否完全充分正确取决于使用者的使用需求。
无限可分性
正态分布是无限可分的概率分布。
稳定性
正态分布是严格稳定的概率分布。
标准偏差
在实际应用上,常考虑一组数据具有近似于常态分布的机率分布。若其假设正确,则约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。